CMU DLSys Course Homework 1: Implementation and Reflection (Part1)

本周看完了课程的 Lecture 3/4/5，这几节课程是对自动求导（Automatic Differentiation）的讲解，其中反向传播、计算图是重点。本文针对 Homework 1 进行实践与思考，其中 Part 1 中包含了 needle 的基本信息和 Question 1 和 Question 2 的内容。

Introduction of Homework 1

通过 Homework 1 自己实践构建一个 needle（Necessary Elements of Deep Learning） 库，其中本文最关键的是自动求导框架的构建，并在 Homework 0 中的双层神经网络上进行应用。

本文对于 needle 的构建是建立在 numpy 库和 CPU 基础上的，后续的作业也会实现相应的底层多维数组以及应用到 GPU 节点上。

Homework 1 的 needle 库包含两个重要的文件，即 autograd.py 和 ops_mathematic.py，其中前者定义了计算图框架以及自动求导框架，后者包含在计算图中会用到的运算符（compute function），及运算符对应的求导函数（gradient function）。

Basic Concept of Needle

本文中应用 needle 库中最重要的几个类包括张量 Tensor 和其继承的父类 Value，以及对应的张量运算符 TensorOp 和其继承的父类 Op。下面对这几个类进行详细解释

Value (the most abstract class)

Value 类是抽象程度最高的类，其实例化的每一个对象都作为计算图中的一个节点（甚至可直接认为其对象代表一个计算图，因为可通过节点进行轨迹追溯）。其中包含四个重要的部分：

• op: Optional[Op] - 该语句定义了节点 Value 所链接的其他节点进行的操作
• inputs: List["Value"] - 包含了计算图中与当前节点相关的节点
• cached_data: NDArray - 该节点存储的具体的值
• requires_grad: bool - 该节点是否需要求导

Tensor (the subclass of value and the interface with user)

Tensor 类是 Value 的子类，并且对应一个实际的张量节点（计算图中的一个多维数组），计算图中实际应用 Tensor 类而非 Value 类。

Op (Operations)

Op 类用于构建计算图中包含的具体的运算符，每一个运算符需要定义计算的前馈函数 compute() 和该运算符对应的求导过程 gradient()，用于后续的反向传播。

TensorOp (the subclass of Op)

TensorOp 类是 Op 的子类，它继承了 Op 中的所有操作符，并且能够返回 Tensor 类型的结果。

在实际运行 needle 库时，需要使用的是 Tensor 类，而 TensorOp 等类都内置于 Tensor 中，以 $c = a + b$ 为例

import needle as ndl
a = ndl.Tensor([1], dtype="float32")
b = ndl.Tensor([2], dtype="float32")
c = a + b # c: Tensor([3], dtype="float32")

上述代码的实际运算过程如下：

1. Tensor.__add__ 调用 Tensor 类中的 "__add__" 方法
2. TensorOp.__call__
3. Tensor.make_from_op(op: Op, inputs: List["Value"]) 首先为 c 实例化了一个新的 Tensor 对象
4. 在返回之前，经过了 Value.realize_cached_data() 或 Tensor.detach() 的计算
5. 进入 Op 类的前馈计算函数中 EWiseAdd.compute 才能得到第 3 步中返回的新 Tensor 对象 c

LAZY_MODE and Detach Function

如下方的代码块所示，为 Value 类中的成员函数 make_from_op()，其中包含了这两个元素

@classmethod
def make_from_op(cls, op: Op, inputs: List["Value"]):
  value = cls.__new__(cls) # create a new object of Value Class
  value._init(op, inputs) # initialize object
  if not LAZY_MODE:
    if not value.requires_grad:
      return value.detach()
    value.realize_cached_data()
  return value

LAZY_MODE 用来控制计算立即执行还是延迟执行。当设置 ndl.autograd.LAZY_MODE = True 时，运行 $c = a + b$ 时并不会立刻进行 realize_cached_data() 的计算，此时的 c.cached_data is None == True，这样只构建计算图但不进行计算，能够有效地优化内存占用，当需要使用 $c$ 的数值时，可以利用 c.data() 来通过前馈计算图获得该节点的 cache_data 数值。

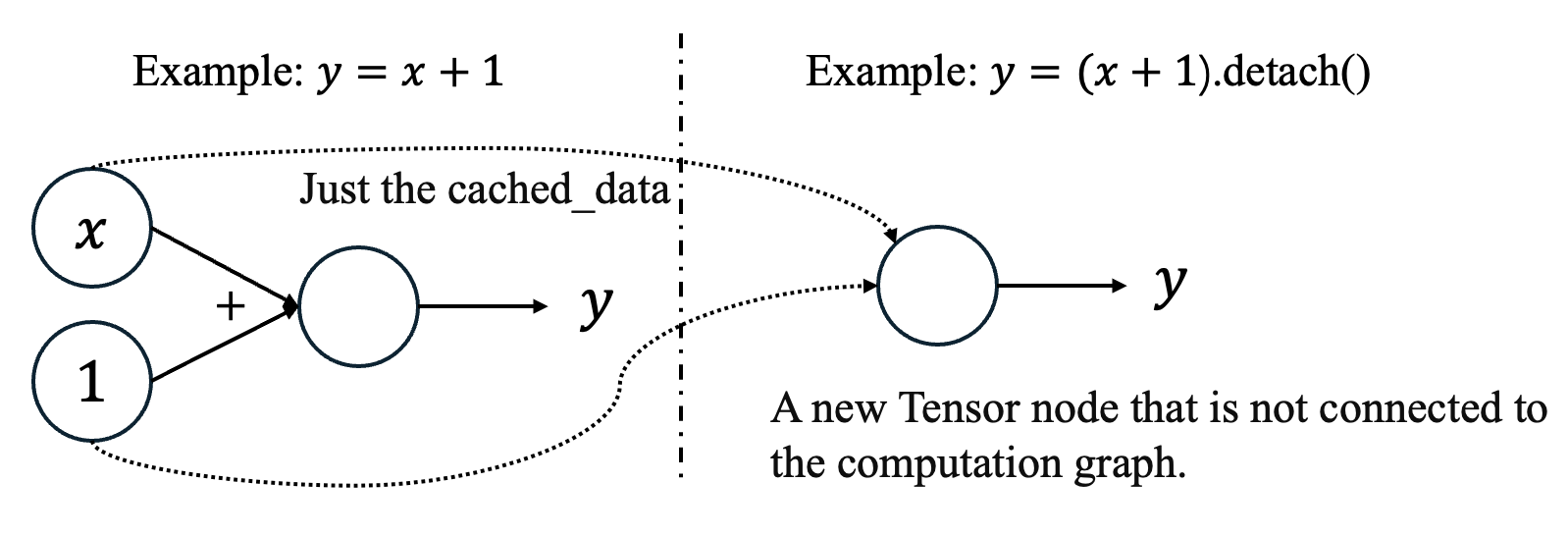
Detach function 用来控制节点是否与计算图链接。如下方的代码所示，虽然看起来简单应该不会占用太多内存，但是由于 Tensor 的计算实质上是对计算图的构建，如图 1 所示，在新节点建立时，背后其实构建了新的计算图，当计算图过多如在迭代中，容易内存/显存溢出。通过 detach 将返回一个新的 Tensor 节点，这个节点孑然一身与其他计算图不相连，即不保留计算图的轨迹。而 detach 是在 requires_grad=False 时才调用的，正因无需计算梯度所以可以只保存为一个单一节点。

for i in range(100):
  sum_loss = sum_loss + x * x

Question 1 & 2: Implementing forward and backward computation

在 needle 中，计算图通过 TensorOp 类下属的各个子类进行实际的张量运算，每一个运算符都具有 compute 成员函数，负责前馈计算，本节的多维数组无需自行构建，而是使用 numpy 的 NDArray 实现，为了后续的移植，以 import numpy as array_api 的形式导入 numpy 包。下面对运算符进行依次实现，在本节的代码中将包含每个运算符类的初始化函数（__init__）、前馈函数（compute）以及求导函数（gradient）。

前馈计算直接按照各运算符的定义执行即可，但每个运算符的求导都较为复杂，需要首先明确的是，该求导的对象是损失函数 loss function $\ell$ 对当前节点 $v_{i+1}$ 的输入节点 $v_i$ 的导数（此处假设 $v_{i+1}$ 仅有一个输入，即 $v_i$，当具有多个输入时，分别计算偏导数即可），$v_{i+1}$ 是其 inputs $v_i$ 在 对应运算符上的函数，即 $v_{i+1}=g(v_{i})$，其中 $\text{out_grad} = \frac{\partial \ell}{\partial v_{i+1}}$，那么导数为

gradient function 会返回的是针对 inputs 中每个节点的偏导数元组。

PowerScalar

对张量进行乘方运算 $X^n$，例如 $X^2=XX^T$，numpy中提供了相应的乘方接口，直接调用即可

下面详细推导张量乘方运算的求导函数，假设计算式为 $v_2=v_1^n$，则 loss function 对 $v_2$ 的导数可计算为

class PowerScalar(TensorOp):
  def __init__(self, scalar:int):
    self.scalar = scalar

  def compute(self, a: NDArray) -> NDArray:
    return array_api.power(a, self.scalar)

  def gradient(self, out_grad, node):
    a = node.inputs[0]
    return out_grad * self.scalar * array_api.power(a, self.scalar - 1)

EWiseDiv

EWise 开头的函数均是逐元素（elementwise）的运算，该函数是对两个张量进行逐元素运算，即 $A \oslash B$

该函数需要考虑分类讨论三种情况：

1. 张量 $A$ 和张量 $B$ 的形状（维度）不同，逐元素的运算要求两张量形状相同
2. 张量 $B$ 的元素全为 0，虽然在 numpy 中会考虑除 0 的情况
3. 正常情况或张量 $B$ 的元素部分为 0

下面详细推导逐元素除法函数的导函数。由于逐元素，因此可以从单个元素的角度来进行计算，其中会使用类似标量的求导法则，对 $v_3=\frac{v_2}{v_1}$ 如下式所示

class EWiseDiv(TensorOp):
  def compute(self, a, b):
    if a.shape != b.shape:
      raise RuntimeError("The shapes of the two tensors are inconsistent.")
    if b.all() == 0:
      raise RuntimeError("All elements of the divisor tensor are zero.")
    return array_api.divide(a, b)

  def gradient(self, out_grad, node):
    lhs, rhs = node.inputs
    return out_grad / rhs, out_grad * lhs / rhs / rhs * (-1)

MatMul

矩阵乘法 $AB$，numpy 在其中的矩阵乘法函数中已经考虑了两个矩阵的形状的约束。

对于该函数的导数，假设 $v_3 = v_1 * v_2$，即 lhs 为 $v_1$，rhs 为 $v_2$，那么

class MatMul(TensorOp):
  def compute(self, a, b):
    return array_api.matmul(a, b)

  def gradient(self, out_grad, node):
    lhs, rhs = node.inputs
    dlhs = array_api.matmul(out_grad, rhs.T)
    drhs = array_api.matmul(lhs.T, out_grad)

    if dlhs.shape != lhs.shape:
      dlhs = summation(dlhs, tuple(range(len(dlhs.shape) - len(lhs.shape))))
    if drhs.shape != rhs.shape:
      drhs = summation(drhs, tuple(range(len(drhs.shape) - len(rhs.shape))))
    assert (dlhs.shape == lhs.shape)
    assert (drhs.shape == rhs.shape)
    return dlhs, drhs

Summation

计算给定轴的和，其中 axes 有多种情况。

1. axes 为单个整数，即按指定轴求和（0（默认值） 为列，1 为行）
2. axes 为元组，如 axes=(0,1)，则沿指定的多个轴求和，在矩阵中此时为求矩阵所有元素的和
3. axes 为 None，即求矩阵的所有元素的和

对于 summation 的导函数，假设输入张量为 $v_i=\mathbb{R}^{n_1\times n_2\times\cdots\times n_k}$，其中对某些维度 axes 进行求和，即 $v_{i+1}=\text{summation}(v_i, \text{axes})$，当 $\text{axes}={d_1,d_2,\cdots,d_m}$时，输出张量的形状应为 $(n_1,n_2,\cdots,n_k)\setminus(n_{d_1},n_{d_2},\cdots,n_{d_m})$，即

class Summation(TensorOp):
  def __init__(self, axes: Optional[tuple] = None):
    self.axes = axes

  def compute(self, a):
    return array_api.sum(a, axes=self.axes)

  def gradient(self, out_grad, node):
    input_shape = node.inputs[0].shape
    shape = list(input_shape)
    if self.axes is not None:
      if isinstance(self.axes, int):
        shape[self.axes] = 1
      else:
        for index in self.axes:
          shape[index] = 1
    else:
      shape = [1 for _ in range(len(shape))]

    out_grad = array_api.reshape(out_grad, shape)
    return out_grad * array_api.ones(input_shape, dtype=array_api.float32)

BroadcastTo

广播机制，将一个较小形状的张量扩展到较大形状的张量。如假设

而期望的形状为 $\mathbb{R}^{2\times 3}$，那么可以将其在 axes=0 的方向复制两次，广播为

class BroadcastTo(TensorOp):
  def __init__(self, shape):
    self.shape = shape

  def compute(self, a):
    return array_api.broadcast_to(a, self.shape)

  def gradient(self, out_grad, node):
    input_shape = node.inputs[0].shape
    output_shape = out_grad.shape
    grad = out_grad
    for i in range(len(output_shape)-len(input_shape)):
      grad = summation(grad, axes=0)
    for index, dim in enumerate(input_shape):
      if dim == 1:
        grad = summation(grad, axes=index)
    return reshape(grad, input_shape)

EWisePow

逐元素乘方，即 $v_3=v_1^{v_2}$，其中 $v_2$ 的元素必须全是整数。前馈函数直接使用 numpy 中的接口即可。下面详细推导求导函数，下面的运算均为逐元素运算

class EWisePow(TensorOp):
  def compute(self, a: NDArray, b: NDArray):
    return array_api.power(a, b)

  def gradient(self, out_grad, node):
    # a^b
    a, b = node.inputs
    if b.dtype.is_integer:
      raise TypeError("dtype should be int!")
    grad_a = out_grad * b * power(a, add(b, -1))
    grad_b = out_grad * power(a, b) * log(a)
    grad_b = array_api.where(a>0, grad_b, 0.0)
    return grad_a, grad_b

本节实现了基本的运算符中的前馈逻辑和求导逻辑，即 Question 1 和 Question 2，其中可能会存在一定的错误，如果您发现了请联系我！谢谢！

Reference

[1] xx要努力. (2022, 11). Deep Learning System-Homework1. 知乎专栏. https://zhuanlan.zhihu.com/p/579465666.

[2] Some parts of the code or math were consulted from ChatGPT and KimiChat.

Contact

There may be some errors present. If you find any, please feel free to contact me at wangqiyao@mail.dlut.edu.cn. I would appreciate it!